Mit unse­rer Tabellierungssoftware GESStabs hal­ten Sie eine umfang­rei­che Software zur Datenaufbereitung in den Händen: neben zahl­rei­chen sta­tis­ti­schen Maßzahlen und Signifikanztests kön­nen Daten berech­net, reko­diert und gewich­tet wer­den. Dies wird mit effek­ti­ven Werkzeugen wie Makros, Overcodes und Filtern erreicht und oben­drein im gewünsch­ten Design, über­sicht­lich und schön dargestellt.

Für die Markt- und Sozialforschung vor­ge­se­hen, ist GESStabs vor­nehm­lich ein Werkzeug für die deskrip­ti­ve Statistik und funk­tio­niert aus­ge­zeich­net zur Ordnung, Darstellung und Beschreibung von Daten. Greifen Sie hier­für bei­spiels­wei­se auf ver­schie­de­ne Streuungsmaße und Kennziffern der zen­tra­len Tendenz zurück.

Zur Verfügung ste­hen außer­dem viel­fäl­ti­ge abhän­gi­ge und unab­hän­gi­ge Signifikanztests für Unterschiede zwi­schen Mittelwerten, Anteilen und gewich­te­te Daten — die­se wer­den von unse­ren Kunden und uns häu­fig und gern genutzt.

Wussten Sie, dass GESStabs noch mehr Mittel zur infe­renz­sta­tis­ti­schen Analyse Ihrer Daten bereit­hält? Schon lan­ge kön­nen im Rahmen von TABLESTATISTICS ver­schie­de­ne Zusammenhangsmaße aus­ge­ben wer­den, etwa Chi², der un-/ stan­dar­di­sier­te Kontingenzkoeffizient und Pearson´s Korrelationskoeffizient r.

Darüber hin­aus haben wir auf einen spe­zi­el­len Kundenwunsch hin das Zusammenhangsmaß Phi als CELLELEMENT ein­ge­führt. Phi ist ein sym­me­tri­sches Zusammenhangs- und Assoziationsmaß, das auf dem Prinzip der Vierfeldertabelle und folg­lich auf der Teststatistik Chi² (im Verhältnis zur Stichprobengröße) basiert. Der Wertebereich von Phi liegt zwi­schen 0 (kein Zusammenhang) und +/- 1 (per­fek­ter Zusammenhang). Die Interpretation des Vorzeichens als posi­ti­ve oder nega­ti­ve Beziehung setzt min­des­tens Ordinalskalenniveau der ein­be­zo­ge­nen Variablen vor­aus, andern­falls soll­te ledig­lich die Zusammenhangsstärke gedeu­tet wer­den. Formell fest­ge­legt ist nur die Interpretation der Extremwerte 0 und 1 — inwie­weit bei­spiels­wei­se ein Wert von 0,2 als gerin­ger, mitt­le­rer oder gro­ßer Zusammenhang gedeu­tet wird, unter­liegt der Abwägung des/r Forschers/in. Eine Ausnahme bil­den dicho­to­me Variablen: hier ent­spricht die Ausprägung und Interpretation von Phi des Korrelationskoeffizienten Pearsons‘s r.

Mit GESStabs lässt sich Phi nun für jede Tabellenzelle ausgeben.
In dem fol­gen­den Beispiel haben wir Daten des Hamburg BUS 2014/15 — einer sozi­al­wis­sen­schaft­li­chen Bürgerumfrage zu Einstellungen, Verhalten und Sozialstruktur der Hamburger Bevölkerung, durch­ge­führt von der Universität Hamburg — ver­wen­det und uns dar­aus eini­ge inter­es­san­te Aussagen zur Benachteiligungserfahrung der befrag­ten Hamburger/innen her­aus­ge­sucht. Ursprünglich auf einer vier­stel­li­gen Likertskala erfasst, haben wir die Antwortkategorien reko­diert in:
1 — trifft auf mich überhaupt/eher nicht zu
2 — trifft auf mich eher/ ganz und gar zu.

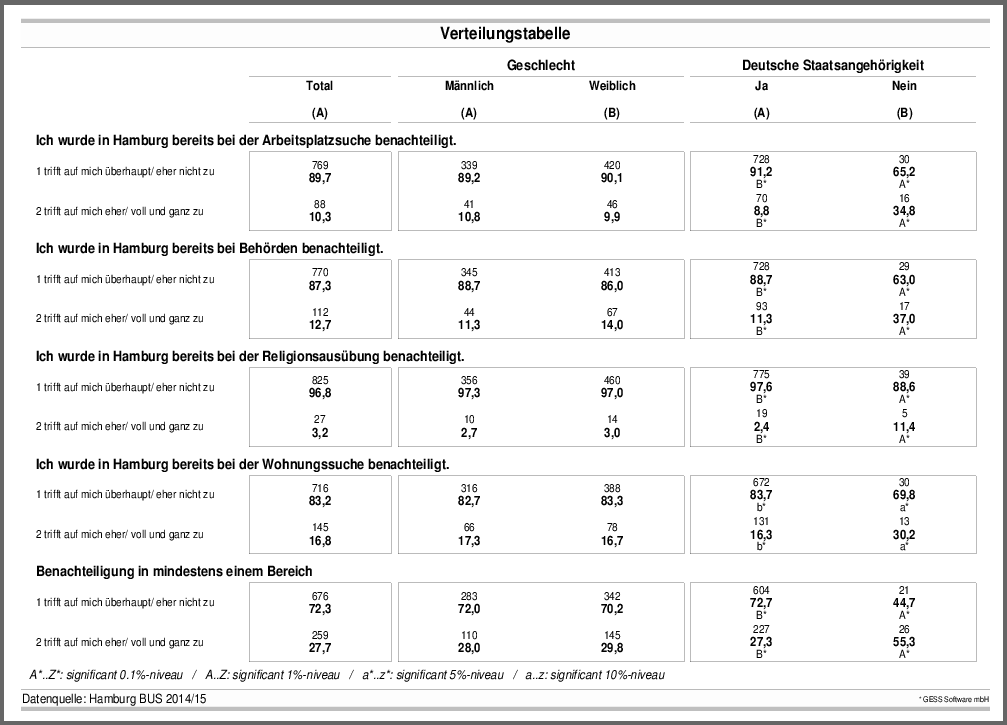
Die unten­ste­hen­de Tabelle zeigt die Verteilung bei­der Kategorien über die Erfahrung von Benachteiligung in ver­schie­de­nen Alltagsbereichen nach Geschlecht und Deutscher Staatsangehörigkeit (ja/ nein), ohne Missing Values und mit Signifikanz-Berechnung (Chi²-Test).

(Klicken Sie auf die Tabelle für eine ver­grö­ßer­te Ansicht.)

Generell gibt die Mehrheit der befrag­ten Hamburger/innen an, über­haupt oder eher kei­ne Benachteiligung bei ihrer Religionsausübung, der Arbeitsplatzsuche, bei Behörden oder der Wohnungssuche erfah­ren zu haben. Allerdings hat ein gutes Viertel bereits Benachteiligung in min­des­tens einem der Bereiche erfah­ren. Zwischen den Geschlechtern gibt es nur mini­ma­le Unterschiede, wohin­ge­gen die Unterschiede zwi­schen Befragten mit und ohne deut­sche Staatsbürgerschaft deut­lich und signi­fi­kant sind. Während die Anteile der befrag­ten deut­schen Staatsbürger/innen, die sich bis­her eher oder über­haupt nicht von Benachteiligung betrof­fen füh­len, leicht über den Anteilen aller Befragten liegt, haben deut­lich mehr Hamburger/innen ohne deut­sche Staatsangehörigkeit bereits Benachteiligung erfah­ren — über die Hälfte in min­des­tens einem die­ser Alltagsbereiche. Auch wenn die abso­lu­ten Fallzahlen hier wesent­lich gerin­ger sind als bei den übri­gen Stichprobenanteilen, gibt jeweils etwa ein Drittel der Befragten mit aus­län­di­scher Staatsbürgerschaft an, bereits bei der Wohnungs- und/ oder Arbeitsplatzsuche sowie bei Behörden benach­tei­ligt wor­den zu sein — die Berechnungen zei­gen signi­fi­kan­te Unterschiede zur Gruppe der Personen mit deut­scher Staatsangehörigkeit.

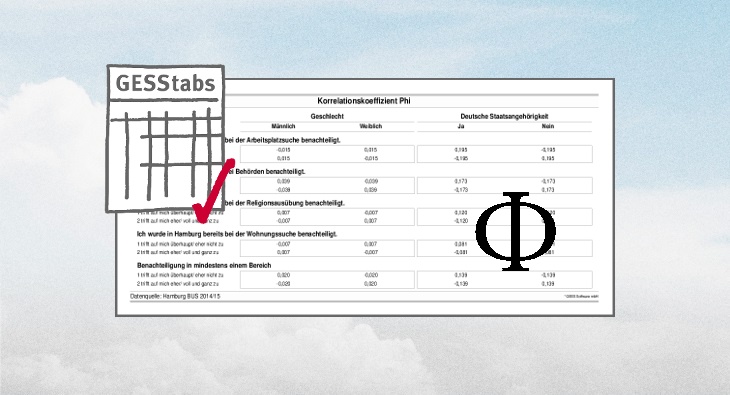
Die Berechnung des Korrelationskoeffizienten Phi zeigt dem­entspre­chend ver­gleichs­wei­se höhe­re Werte für die Kreuzung von ‘Deutsche Staatsangehörigkeit’ und Benachteiligungserfahrung als für sel­bi­ges und das Geschlecht.

(Klicken Sie auf die Tabelle für eine ver­grö­ßer­te Ansicht.)

Während hin­sicht­lich der Wohnungssuche und Religionsausübung kein nen­nens­wer­ter sta­tis­ti­scher Zusammenhang besteht, zei­gen Werte von jeweils +/- 0,173 bzw. +/- 0,195, dass zumin­dest ein schwa­cher Zusammenhang zwi­schen der Benachteiligungserfahrung bei Behörden bzw. der Arbeitsplatzssuche und der Tatsache, ob man deut­scher Staatsbürger ist, vor­han­den ist.
Dass je nach betrach­te­ter Zelle für die­sel­ben Variablen Phi mal posi­tiv, mal nega­tiv aus­ge­prägt ist, macht sta­tis­tisch und inter­pre­ta­tiv natür­lich Sinn: Je nach­dem, ob eine deut­sche Staatsbürgerschaft vor­han­den ist, ist die Wahrscheinlichkeit, schon ein­mal benach­tei­ligt wor­den zu sein, klei­ner oder größer.

Eine Bemerkung: In der sozi­al­wis­sen­schaft­li­chen Forschung wer­den wir mit hohen Zusammenhangsmaßen nicht gera­de ver­wöhnt — das liegt in der Natur des Forschungsgegenstandes, sagt aber natür­lich zunächst nichts über des­sen inhalt­li­che Relevanz aus.  Sicher fin­den Sie in Ihrer markt­for­sche­ri­schen Tätigkeit höhe­re Zusammenhänge für ande­re betrach­te­te Gegenstände. Die oben ste­hen­de Analyse dient jedoch als gutes (und, wie wir fin­den: inter­es­san­tes) Beispiel, wie eine klei­ne Zusammenhangsanalyse mit­hil­fe von GESStabs aus­se­hen kann.

Eine wei­te­re Möglichkeit zum sinn­vol­len Einbezug von Phi in Ihre Analyse mit GESStabs wäre im Rahmen einer Faktoranalyse: Indem Variablen (mit Phi als CELLELEMENT ) gegen sich selbst tablliert wer­den, kann eine Korrelationsmatrix erzeugt und ein ers­tes Gefühl für das Verhältnis der ein­zu­be­zie­hen­den Variablen bekom­men erhal­ten werden.

Quelle zu Phi: Steffen‑M. Kühnel & Dagmar Krebs (2007): Statistik für die Sozialwissenschaften. Grundlagen, Methoden, Anwendungen. 4. Auflage. Reinbek bei Hamburg: Rowohlt Taschenbuch Verlag.

Datenquelle: Hamburg BUS 2014/15, Bürgerumfrage der Sozialwissenschaften für Hamburg. Quelle: Olaf Bock; Kay-Uwe Schnapp; Jan Papmeier; Universität Hamburg (2015): Hamburg BUS 2014. Version: 1. GESIS Datenarchiv. Datensatz. URL: http://doi.org/10.7802/79.